In this talk, we explore Linearized Reactive Field (LRF) methods and their developing role in comprehending the dynamics of turbulent combustion. We will begin with a brief overview of linearized mean field methods, highlighting their significance in revealing the importance of coherent structures in turbulent flows. We will explore key theoretical concepts integral to our approach, such as triple decomposition, linear stability, and resolvent analysis. To begin, we will examine nonreacting flows, using amplifier and oscillator flows as examples. From there, we will move on to reacting flows, where we will introduce fundamental equations and address the multi-closure problem, a major hurdle in the modelling of combustion dynamics. Emphasis will be placed on the innovative approach of data assimilation as a means of effectively addressing this closure problem. We detail the suite of tools developed for studying LRF methods to facilitate their implementation and comprehension. These tools incorporate various techniques, such as combustion experiments, Large Eddy Simulations, Physics-Informed Neural Networks, and the Finite Element Linearized Reacting Field Solver (FELICS). The presentation will illustrate multiple examples of LRF techniques in the field of combustion dynamics, which tackle the propagation of entropy and swirl fluctuations, as well as turbulent flow-flame interactions. To summarise, a future outlook will be provided on LRF application, with a particular focus on the transition to hydrogen combustion.
Archives : Évènements
Dispersive non-linear water waves in arbitrary cross-sectional channels
Weakly dispersive, fully nonlinear waves in channels of arbitrary cross-section are considered from a variational viewpoint. A set of general equations is derived, that resemble the Serre-Green-Naghdi equation. Traveling wave solutions in prismatic channels are derived in the form of pseudo-elliptic integrals. The case of solitary waves in trapezoidal channels is addressed more deeply, with comparison to experiments as regards the celerity of the leading wave in an undular bore.
Leveraging physics-based models and data to capture complex combustion multi-physics for clean, decarbonized energy systems
The need to regulate greenhouse gas emissions has driven the search for clean and efficient energy solutions, requiring the integration of alternative fuels for a sustainable future. Alternative fuels (hydrogen, ammonia, biofuels, Sustainable Aviation Fuels, SAF) present different attributes with respect to traditional hydrocarbon fuels, such as burning rate and pollutant emissions, leading to new challenges. Undertaking these tasks involves the need for numerical combustion modeling and, due to the complexity of such systems, sophisticated strategies for efficient simulations. In this context, soot formation has been considered a major challenge due to its complex nature, and that would still be present in future energy systems (e.g., biofuels or SAF). As a first part of the presentation, I will introduce two different approaches of soot modeling. The first one is the so-called virtual chemistry approach, developed at EM2C. This method involves the creation of a global mechanism comprising virtual species and reactions. Machine learning algorithms optimize the thermodynamic properties and kinetic rate parameters of these virtual components. This methodology primarily focuses on capturing essential sooting flame properties such as temperature, laminar flame speed, radiation, and soot volume fraction. It has been adapted for the simulation of turbulent sooting flames using Large Eddy Simulation (LES), which I will exhibit with further details. The second approach, developed more recently at Princeton, is called Bivariate Multi-Moment Sectional Method (BMMSM). BMMSM is designed for computationally efficient tracking of soot size distribution in turbulent reacting flows. It combines the sectional method with the method of moments to characterize the size distribution. Notably, BMMSM employs fewer soot sections compared to traditional sectional models while considering three volume-surface moments per section to account for soot’s fractal aggregate morphology. Then, I will present LES results of the evolution of the soot size distribution in a turbulent nonpremixed flame. In the second part of this presentation, I will present insights into the emissions from the combustion of other candidate fuels, including recent work on the use of ammonia, determining if they exhibit sufficiently low levels compared to current fuels, while minimizing societal and environmental impacts. Then, I will present simulation results of partially cracked ammonia combustion, which are representative of the design of future gas turbines for power production, to identify the mechanisms behind the production of other carbonless greenhouse gases, such as N2O, and pollutants, such as NOx, and how they might compare with the emission trends associated with traditional hydrocarbon fuels. Finally, a few points highlighting that the needs and challenges in combustion science are evolving will be discussed.
La diffusion Rayleigh pour le diagnostic optique des écoulements, principes et applications pour l’aéroacoustique et la turbulence thermique
La diffusion Rayleigh est le mode de la diffusion d’une onde électromagnétique par des particules petites devant la longueur d’onde considérée. Dans le contexte du diagnostic optique des écoulements, l’onde est généralement issue d’une source laser dans le visible, et les particules sont les molécules constituantes du gaz. Il n’y a donc aucun traceur non intrinsèquement déjà présent dans l’écoulement, ce qui en fait une méthode particulièrement adaptée aux écoulements rapides. Un panel de techniques découle de l’étude de la lumière diffusée par les molécules. Nous nous intéresserons en particulier à l’intensité de celle-ci qui permet de mesurer la masse volumique locale d’un écoulement, avec deux applications.
– l’étude des corrélations entre les fluctuations hydrodynamiques dans un jet à Mach 0.9 et le rayonnement acoustique vers l’aval.
– la mesure des fluctuations de température des fréquences de plusieurs kilohertz dans le sillage d’un barreau chauffé (Mach ~0.01).
Nous évoquerons aussi les méthodes basées sur l’analyse spectrale du rayonnement, qui permettent en principe d’obtenir la température et la vitesse locale en plus de la masse volumique.
Dispersive censor of acoustic spacetimes with a shock-wave singularity
A dispersionless shock wave in a fluid without friction develops an acoustic spacetime singularity which is naked (not hidden by a horizon). We show that this naked nondispersive shock-wave singularity is prohibited to form in a Bose-Einstein condensate, due to the microscopic structure of the underlying aether and the resulting effective trans-Planckian dispersion. Approaching the instant
of shock t_shock, rapid spatial oscillations of density and velocity develop around the shock location, which begin to emerge already slightly before t_shock}, due to the quantum pressure in the condensate. These oscillations render the acoustic spacetime structure completely regular, and therefore lead to a removal (censoring) of the spacetime singularity. Thus, distinct from the cosmic censorship hypothesis of Penrose formulated within Einsteinian gravity, the quantum pressure in Bose-Einstein
condensates censors (prohibits) the formation of a naked shock-wave singularity, instead of hiding it behind a horizon.
Bayesian Inference for Construction of Inverse Models from Data
This talk considers the inverse problem y=f(x), where x and y are observable parameters, in which we wish to recover the model f. Examples include dynamical systems and combat models with y=dx/dt and x=parameter(s), water catchments with y=streamflow and x=rainfall, and groundwater vulnerability with y=pollutant concentration(s) and x=hydrological parameter(s). Historically, these have been solved by many methods, including regression or sparse regularization for dynamical system models, and various empirical correlation methods for rainfall-runoff and groundwater vulnerability models. These can instead be analyzed within a Bayesian framework, using the maximum a posteriori (MAP) method to estimate the model parameters, and the Bayesian posterior distribution to estimate the parameter variances (uncertainty quantification). For systems with unknown covariance parameters, the joint maximum a-posteriori (JMAP) and variational Bayesian approximation (VBA) methods can be used for their estimation. These methods are demonstrated by the analysis of a number of dynamical and hydrological systems.
Séminaire Équipe TriboLub, le 15 juin à 10h, H1
Mihai Arghir : Comparaison entre les méthodes d’homogénéisation et multi-échelles pour l’analyse d’écoulements compressibles entre surfaces rugueuses
La présentation porte sur une comparaison entre la méthode de l’homogénéisation et une méthode multi-échelles appliquées à l’équation de Reynolds compressible à coefficients irréguliers. L’équation modélise un écoulement compressible entre des surfaces rugueuses très peu espacées. L’utilisation de la méthode d’homogénéisation pour l’équation de Reynolds à coefficients irréguliers n’est pas nouvelle. La méthode multi-échelles est empruntée aux écoulements en milieu poreux (où seuls les écoulements dus aux gradients de pression sont présents) et est ici étendue pour prendre également en compte les termes de Couette. Le développement des deux méthodes est présenté en soulignant les similitudes et les différences. Des résultats illustratifs obtenus pour une géométrie réaliste montrent l’impact du maillage grossier, de la précision de la solution sur le maillage fin et l’effort de calcul des deux méthodes par rapport à l’équation de Reynolds compressible originale.
Charles Aboussafy: Une méthode de calcul découplée, basée sur la pression pour modéliser la cavitation en régime stationnaire – une stratégie de modélisation par éléments finis appliquée aux paliers
Cette étude présente un modèle de cavitation appliqué aux équations de Navier-Stokes dans des conditions stationnaires. Le développement du modèle proposé vise l’étude de systèmes avec des surfaces texturées, où l’équation de Reynolds ne peut pas être utilisée pour produire des évaluations précises. En effet, l’équation de Reynolds est efficace dans des plages restreintes de vitesses et pour des rapports limités des dimensions d’une texture. L’approche développée élimine ces limitations. Au lieu d’utiliser une approche par la méthode des volumes finis couramment utilisée en CFD, le modèle proposé est basé sur une discrétisation par éléments finis. La phase de cavitation est modélisée par une formulation barométrique. Par rapport aux modèles utilisant l’équation de Rayleigh-Plesset, l’avantage de la méthode proposée est qu’aucun paramètre ne doit être adapté expérimentalement. Les résultats préliminaires obtenus concordent à la fois avec les évaluations expérimentales et numériques extraites des articles de référence. En particulier, les pressions prédites sont en parfait accord avec les résultats numériques de référence présentés pour les paliers.
Séminaire Équipe TriboLub, le 17 mai 2023 à Angoulême
Deux présentations seront au programme :
ON THE USE OF SUPERSONIC JET-CURTAINS FOR CONTROL OF MOMENTS ON TAILLESS AIRCRAFT
The purpose of this study is to explore the replacement of conventional moving control surfaces on a typical tailless aircraft model at high subsonic cruise speeds. Since the efficacy of sweeping jet actuators was only demonstrated at low speeds, the current test considered their potential replacement by Supersonic Steady Jets (SSJs). It was shown that even a single jet properly located and oriented may outperform an array of actuators whose location and orientation did not take into consideration the changing local flow conditions. The test article chosen was the SWIFT model that represents a typical blended wing-body configuration of a tailless aircraft. It was selected because it was tested extensively using Sweeping Jet Actuators (SJAs). When a single supersonic jet designed for Mn=1.5 was used to control thepitch it was able to increase the trimmed lift by approximately a factor of 3. The power it consumed was not necessarily smaller than an array of 6 SJAs but it provided other advantages that are discussed in the paper. Large yawing moments could be provided by other SSJs that were not encumbered by large rolling moments. These tests proved that the momentum input is but one of many parameters controlling the flow. It was replaced by power coefficients that are unambiguously measured and are capable of comparing various modes of actuation.
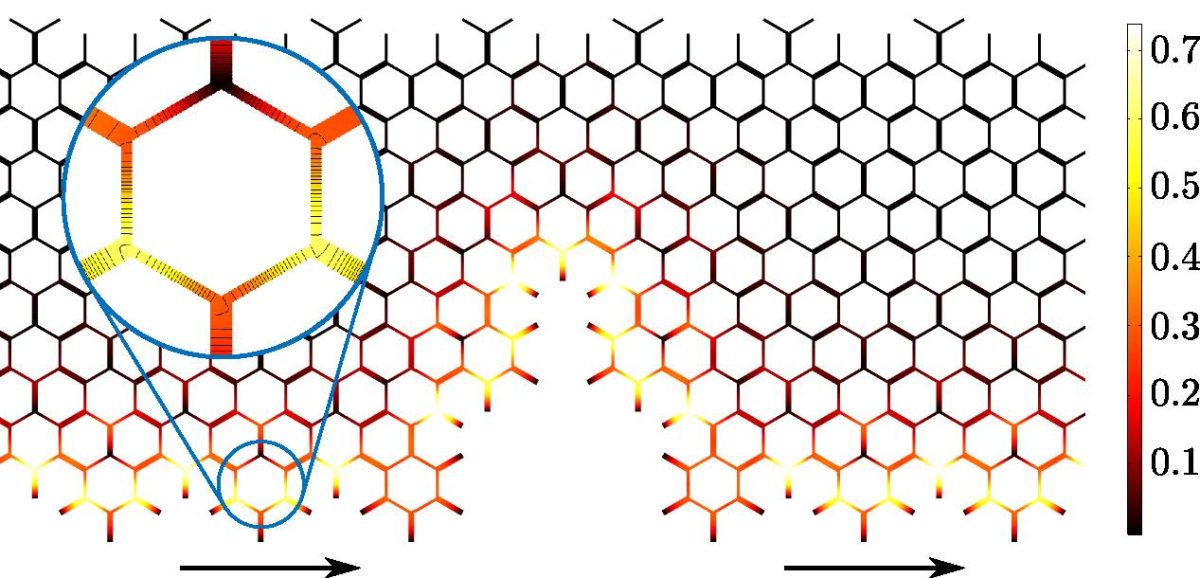
Scattering of topological edge waves in Kekule structures
Kekule structures are graphene-like lattices, with a modulation of the intersite coupling that preserves the hexagonal symmetry of the system. These structures possess very peculiar properties. In particular, they display topological phases manifested by the presence of edge waves propagating on the edge of a sample. We will discuss the extraordinary scattering properties of these edge waves across defects or disorder. We will also discuss how to realize Kekule structures in acoustic networks of waveguides